Chapter 3 Plug-in Classifiers (Similarity Classifier)

For binary classification with 0-1 loss:

1. \(\mathfrak f_B(x)\) = \(\begin{cases}1 & if ~P_{(X,Y) \in \rho}(Y=1 \mid X=x) \geq P_{(X,Y) \in \rho}(Y=0 \mid X=x)\\0 & o.w.\end{cases}\) is Motivate “plug-in” or similarity classifier;

2. \(\mathfrak f_B \in \underset{\mathfrak f: \mathcal X \to \{0,1\}}{\operatorname{argmin}} ~ P(\mathfrak f(X) \neq Y)\) is Motivate ERM (Empirical Risk Minimization).

For this chapter, we will talk about the first one.

Define \(\eta(x) := P(Y=1 \mid X=x)\), then we can rewrite \(\mathfrak f_B(x)\) as: \(\mathfrak f_B(x) = \begin{cases}1 & \eta(x) \geq \frac{1}{2}\\0 & o.w.\end{cases}.\)

Idea: Replace \(\eta(x)\) with \(\hat \eta_n(x)\) that is built from our training data \((x_1,y_1), \cdots, (x_n,y_n)\): \(\hat{\mathfrak f}_n(x) = \begin{cases}1 & \hat \eta_n(x) \geq \frac{1}{2}\\0 & o.w.\end{cases}.\)

Lemma 3.1 Let \(\mathfrak f\) be an arbitrary binary classifier. Then

\[ 0 \leq R(\mathfrak f) - R_B^* = E\Big[\mid 2 \eta(X) - 1 \mid \cdot 1_{\mathfrak f(X) \neq \mathfrak f_B(X)}\Big] \leq 2 E\Big[ \mid \eta(X) - \alpha(X) \mid \Big], \]

where we suppose \(\mathfrak f(X) = \begin{cases}1 & \alpha(X) \geq \frac{1}{2}\\0 & o.w.\end{cases}.\)

Proof. As

\[ \begin{aligned} E[1_{\mathfrak f(X) \neq Y} - 1_{\mathfrak f_B(X) \neq Y} \mid X] &= (1_{\mathfrak f(X) \neq 1} - 1_{\mathfrak f _B(X) \neq 1}) \cdot P(Y=1 \mid X) + (1_{\mathfrak f(X) \neq 0} - 1_{\mathfrak f _B(X) \neq 0}) \cdot P(Y=0 \mid X)\\ &= (1_{\mathfrak f(X) \neq 1} - 1_{\mathfrak f _B(X) \neq 1}) \cdot \eta(X) + (1_{\mathfrak f(X) \neq 0} - 1_{\mathfrak f _B(X) \neq 0}) \cdot (1-\eta(X))\\ &= \begin{cases} 0 & if ~ \mathfrak f(X) = \mathfrak f_B(X) = 1\\ 0 & if ~ \mathfrak f(X) = \mathfrak f_B(X) = 0\\ \mid 1-2\eta(X) \mid & if ~ \mathfrak f(X) =1,~ \mathfrak f_B(X) = 0\\ \mid 2\eta(X)-1 \mid & if ~ \mathfrak f(X) =0,~ \mathfrak f_B(X) = 1\\ \end{cases}\\ &= \mid 2\eta(X)-1 \mid \cdot 1_{\mathfrak f(X) \neq \mathfrak f_B(X)}, \end{aligned} \]

we have:

\[ \begin{aligned} R(\mathfrak f) - R_B^* &= E\Big[E[1_{\mathfrak f(X) \neq Y} - 1_{\mathfrak f_B(X) \neq Y} \mid X] \Big]\\ &= E\Big[\mid 2 \eta(X) - 1 \mid \cdot 1_{\mathfrak f(X) \neq \mathfrak f_B(X)}\Big]. \end{aligned} \]

Moreover,

• Case1: \(\mathfrak f(X) \neq \mathfrak f_B(X)\), \(\eta(X) < \frac{1}{2}\)
  In this case, \(\mathfrak f_B(X) = 0\) and \(\mathfrak f(X) = 1\), which means that \(\alpha(X) \geq \frac{1}{2}\). So, \(2 \mid \eta(X) - \frac{1}{2} \mid \leq 2 \mid \eta(X) - \alpha(X) \mid\).

• Case 2: \(\mathfrak f(X) \neq \mathfrak f_B(X)\), \(\eta(X) \geq \frac{1}{2}\)
  Similarly, we have \(2 \mid \frac{1}{2} - \eta(X) \mid \leq 2 \mid \eta(X) - \alpha(X) \mid\).

Thus, \(E\Big[\mid 2 \eta(X) - 1 \mid \cdot 1_{\mathfrak f(X) \neq \mathfrak f_B(X)}\Big] \leq 2E\Big[\mid \eta(X) -\alpha(X) \mid \cdot 1_{\mathfrak f(X) \neq \mathfrak f_B(X)}\Big].\)

Corollary 3.1 If \(\hat{\mathfrak f}_n(X) = \begin{cases}1& if~ \hat \eta_n(X) \geq 1/2 \\0 & o.w.\end{cases}\), \(\hat \eta_n(X) = \hat \eta_n (X; (x_1, y_1), \cdots, (x_n, y_n))\), then

\[ E[R(\hat{\mathfrak f}_n)] - R^*_B \leq 2 E\Big[\mid \eta(X) - \hat \eta_n(X) \mid\Big]. \]

Remark. For \(\hat{\mathfrak f}_n\), \(\eta(X)\), and \(\hat \eta_n(X)\), we have \((X, Y) \sim \rho\) and \((x_1, y_1), \cdots, (x_n, y_n) \sim \rho\).

Proof. Given \((x_1, y_1), \cdots, (x_n, y_n)\), according to Lemma 3.1, we have: \(R(\hat{\mathfrak f}_n) - R^*_B \leq 2 E\Big[\mid \eta(X) - \hat \eta_n(X) \mid\Big]\).

In general, we are interested in building classifier from observation \((x_1, y_1), \cdots, (x_n, y_n)\): \(\hat {\mathfrak f}_n: ~\mathcal X \to \{0,1\}\), \(\hat {\mathfrak f}_n (X) \in \{0,1\}\).

---

Example 3.1 (Dependency on Data) Given \((x_1, y_1), \cdots, (x_n, y_n)\),

\[ \hat \eta_n(X) := \frac{\sum_{i=1}^n Y_i exp(-\mid X_i - X \mid ^2 / r_n^2)}{\sum_{i=1}^n exp(-\mid X_i - X \mid ^2 / r_n^2)}. \]

Then we have:

\[ \hat {\mathfrak f}_n(X; (x_1, y_1), \cdots, (x_n, y_n)) = \begin{cases} 1 & if ~\hat \eta_n(X) \geq \frac{1}{2}\\ 0 & o.w. \end{cases} \]

---

Remark. \(\hat \eta_n(X) \in [0,1]\).

Goal: To build \(\hat{\mathfrak f}_n\) in such a way that \(R(\hat{\mathfrak f}_n) - R^*_B\) goes to 0 as \(n \to \infty\).

3.1 Notions of Consistency for Families of Binary Classifier

1. We say that \(\{\hat{\mathfrak f}_n\}_{n\in N}\) is consistent for the distribution \(\rho\), if we have:
   \[ \underset{n \to \infty}{\operatorname{lim}} (E_{(x_1, y_1), \cdots, (x_n, y_n)} [R(\hat{\mathfrak f}_n)] - R^*_B) = 0 \]

Remark.

• \((x_1, y_1), \cdots, (x_n, y_n) \underset{i.i.d}{\sim} \rho\).

• \(R^*_B = \underset{\mathfrak f}{\operatorname{min}} P_{(X,Y) \sim \rho} [\mathfrak f(X) \neq Y]\).

• \(R(\hat{\mathfrak f}_n) = P_{(X,Y) \sim \rho} [\hat{\mathfrak f}_n(X) \neq Y]\).

2. We say that \(\{\hat{\mathfrak f}_n\}_{n\in N}\) is strongly consistent for the distribution \(\rho\), if we have:
   \[ \underset{n \to \infty}{\operatorname{lim}} (R(\hat{\mathfrak f}_n) - R^*_B) = 0, ~\text{with probability 1 (almost sure convergence).} \]

---

Example 3.2 (Conceptual Explaination) Assume we have M students.Then for student m, we have:

\[ \begin{cases} (x_1^m, y_1^m), \cdots, (x_n^m, y_n^m) \underset{i.i.d}{\sim} \rho\\ \text{The plug-in classifier}: ~\hat{\mathfrak f}_n^m (\cdot ~;(x_1^m, y_1^m), \cdots, (x_n^m, y_n^m))\\ \text{Risk: }R(\hat{\mathfrak f}_n^m) = P_{(X,Y) \sim \rho} [\hat{\mathfrak f}_n^m(X) \neq Y] \end{cases}. \]

Q1 (Consistency): Suppose I collect all risks that the class computed: \(R(\hat{\mathfrak f}_n^1), \cdots, R(\hat{\mathfrak f}_n^M)\), and suppose I average them: \(\frac{1}{M} \sum_{m=1}^M R(\hat{\mathfrak f}_n^m) \approx E_{(x_1, y_1), \cdots, (x_n, y_n)} [R(\hat{\mathfrak f}_n)]\). Is it true that as \(n \to \infty\), this average risk goes to \(R^*_B\).

Q2 (Strong Consistency): Is it true that for each \(m\), we have that \(R(\hat{\mathfrak f}_n)\) converges to \(R^*_B\) as \(n \to \infty\).

---

3. We say that a family \(\{\hat{\mathfrak f}_n\}_n\) is universal (strong) consistent if \(\{\hat{\mathfrak f}_n\}_n\) is (strong) consistent for all \(\rho\).

---

Example 3.3 (Universality in Statistical Inference) Let \(\mu\) be a probability distribution over \(R\) with well defined first moment \(\theta := E_{Z \sim \mu} (Z)\). The goal is to build an estimator \(\hat \theta_n(z_1, \cdots, z_n)\) that is consistent for \(\theta\).

• \(\hat \theta_n^1(z_1, \cdots, z_n) = \frac{1}{n} \sum z_i ~(\text{Sample Mean})\), is universal strong consistent.
  \(z_1, \cdots, z_n \underset{i.i.d}{\sim} \mu\) for arbitrary \(\mu\), by Law of Large Number (Strong LLN), we know that with probability 1, \((\hat \theta_n^1(z_1, \cdots, z_n) - \theta) \to 0\) as \(n \to \infty\).

• \(\hat \theta_n^2(z_1, \cdots, z_n) = \text{Sample Median}\), is not universal consistent.
  If \(\mu\) is a distribution such that its median is not equal to its mean, then it is not true that \((\hat \theta_n^2(z_1, \cdots, z_n) - \theta) \to 0\) as \(n \to \infty\). However, \(\hat \theta_n^2(z_1, \cdots, z_n)\) is consistent for \(\mu = N(1,1)\) whose mean and median are the same.

---

For the plug-in classifiers, studying (strong) consistency reduce to understanding the following two questions:

• Does \(E_{(X,Y) \sim \rho} \Big[\mid \eta(X) - \hat \eta_n(X) \mid \Big]\) converge to 0 as \(n \to \infty\), with probability 1?
  If yes, \(\{\hat{\mathfrak f}_n\}_n\) is strong consistent for \(\rho\).

• Does \(E_{(x_1,y_1), \cdots, (x_n,y_n), (X,Y) \sim \rho} \Big[\mid \eta(X) - \hat \eta_n(X) \mid \Big]\) converge to 0 as \(n \to \infty\)?
  If yes, \(\{\hat{\mathfrak f}_n\}_n\) is consistent for \(\rho\).

3.2 Functions of \(\hat \eta_n\)

\[ \hat \eta_n(X; (x_1,y_1), \cdots, (x_n,y_n)) = \sum_{i=1}^n y_i \omega_{in} (X; x_1, \cdots, x_n) \]

where \(\omega_{in} (X; x_1, \cdots, x_n)\) is weight that we give to each point \((x_i, y_i)\) and \(\sum_{i=1}^n \omega_{in} (X; x_1, \cdots, x_n) = 1\).

In other words, to determine \(\hat \eta_n(X)\), we consider weighted averages of the labels \(y_1, \cdots, y_n\).

Intuitively the \(i\)s for which \(\omega_{in}\) are larger should be ones for which \(x_i\) is more similar to \(X\).

---

Example 3.4 (Kernel-Based Weights) \(\mathcal X = R^d\), select a length-scale \(r > 0\).

\[ \omega_{in}(X; x_1, \cdots, x_n) = \frac{exp(- \frac{|| X_i - X || ^2}{2r^2}) }{\sum_{i=1}^n exp(-\frac{|| X_i - X || ^2}{2r^2})}. \]

Points \(x_i\) for which \(|| X - x_i || \leq r\) will be give higher weight than points that are such that \(|| X - x_i || \geq r\).

---

Example 3.5 (Histogram-Based Weights) \(\mathcal X = R^d\), select a length-scale \(h > 0\).

For \(d=2\), we have:

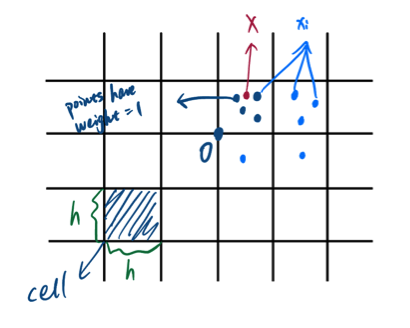
Introduce pre-weights:

Provided there is at least one \(x_i\) in the same cell as \(X\):

\[ \tilde \omega_{in}(X; x_1, \cdots, x_n) := \begin{cases} 1 & \text{if } x_i \text{ and } X ~\text{belong to the same cell}\\ 0 & o.w. \end{cases} \] Otherwise we define:

\[ \tilde \omega_{in}(X; x_1, \cdots, x_n) := \frac{1}{n} \] Then we have:

\[ \omega_{in}(X; x_1, \cdots, x_n) = \frac{\tilde \omega_{in}(X; x_1, \cdots, x_n)}{\sum_{j=1}^n \tilde \omega_{jn}(X; x_1, \cdots, x_n)} \]

---

Example 3.6 (k-NN Based Weights) \(k \in [1,n]\)

\[ \tilde \omega_{in}(X; x_1, \cdots, x_n) = \begin{cases} 1 & \text{if } x_i \text{ is among the k-closest points to } X\\ 0 & o.w. \end{cases} \] Then we have:

\[ \omega_{in}(X; x_1, \cdots, x_n) = \frac{\tilde \omega_{in}(X; x_1, \cdots, x_n)}{\sum_{j=1}^n \tilde \omega_{jn}(X; x_1, \cdots, x_n)} \]

There may be ties, which will be discussed later.

---

3.3 Consistency

Theorem 3.1 (Stone's Theorem) Let \(\omega_{in}(X; x_1, \cdots, x_n)\) be such that following three conditions hold:

1. \(\exists c>0\) such that \(\forall \text{non-negative function } g: R^d \to R\), with \(E_{(X,y) \sim \rho} [g(X)] < \infty\): \(E_{(X, x_1, \cdots, x_n)} [\sum_{i=1}^n \omega_{in} (X) g(x_i)] \leq c ~E_X [g(X)]\);

2. \(\forall a > 0\), \(\underset{n \to \infty}{\operatorname{lim}} E_{(X, x_1, \cdots, x_n)} [\sum_{i=1}^n \omega_{in}(X) ~1_{|x_i - X| > a}] = 0\) (weights are only relevant or large for \(x_i\) close to \(X\));

3. \(\underset{n \to \infty}{\operatorname{lim}} E_{(X, x_1, \cdots, x_n)} [\underset{i=1,\cdots, n}{\operatorname{max}} \omega_{in}(X)] = 0\).

Then the family of similarity classifiers \(\{\hat{\mathfrak f}_n\}_n\) induced by these weights is consistent for \(\rho\).

Proof.

Goal: to show that \(E_{(X,Y), (x_1,y_1), \cdots, (x_n, y_n)} [|\eta(X) - \hat \eta_n(X)|] \to 0\) as \(n \to \infty\).

Introduce \(\bar \eta_n(X) := \sum_{i=1}^n \eta(x_i) \omega_{in}(X)\), then

\[ \begin{aligned} E_{(X,Y), (x_1,y_1), \cdots, (x_n, y_n)} [|\eta(X) - \hat \eta_n(X)|] &\leq E_{(X,Y), (x_1,y_1), \cdots, (x_n, y_n)} [|\eta(X) - \bar \eta_n(X)|] + \\ &\quad E_{(X,Y), (x_1,y_1), \cdots, (x_n, y_n)} [|\bar \eta_n(X) - \hat \eta_n(X)|]\\ &\underset{C.S. Ineq}{\leq} E_{(X,Y), (x_1,y_1), \cdots, (x_n, y_n)} [|\eta(X) - \bar \eta_n(X)|] \text{ ("bias term")}+ \\ &\quad \Big(E_{(X,Y), (x_1,y_1), \cdots, (x_n, y_n)} [|\bar \eta_n(X) - \hat \eta_n(X)|^2]\Big)^2 \text{ ("variance term")} \end{aligned} \]

Then show both terms \(\to 0\) as \(n \to \infty\).

Remark.

1. \[ \begin{aligned} E[\hat \eta_n(X) | X, x_1 \cdots, x_n] &= \sum_{i=1}^n E[y_i | X, x_1, \cdots, x_n] ~\omega_{in}(X)\\ &= \sum_{i=1}^n E[y_i | X, x_1, \cdots, x_n] ~\omega_{in}(X)\\ &= \sum_{i=1}^n E[y_i | x_i] ~\omega_{in}(X)\\ &= \bar \eta_n(X) \end{aligned}; \]

2. To show that the variance term \(\to 0\) as \(n \to \infty\), we only need to use condition 3 in the Theorem 3.1;

3. To show that the bias term \(\to 0\) as \(n \to \infty\), we only need to use conditions 1 and 2 in the Theorem 3.1.

Example 3.7 (Continuation of Example 3.5) Let \(h^d = h_n^d\). If \(n h_n \to \infty\) as \(n \to \infty\), and if \(h_n^d \to 0\) as \(n \to \infty\), then the family of histogram classifiers \(\{\hat {\mathfrak f}_{n, h_n}\}_{n \in N}\) is universally consistent.

Conditions of the Stones Theorem:

1. Technical Assumption.

2. Locality (\(h = h_n \to 0\) as \(n \to \infty\)).

3. No weight dominates the others. (For every \(X\), we should use a growing number of training data points to make a prediction, i.e. the expected number of points in a cell \(nh_n^d \to \infty\) as \(n \to \infty\))

For example, let \(\rho = Uniform\), \(N_X = \#\{x_i ~s.t. ~x_i \in Cell(X)\}\), then \(N_X \sim Binomial(n, P_h)\), where \(P_h = P(x_i \in Cell(X)) \propto h^d\). As a result, \(E(N_X) \propto nh^d\).

Example 3.8 (Continuation of Example 3.6)

• \(k \to \infty\) (locality)

• \(\frac{k}{n} \to 0\) (Related to condition 3 in Stone’s Theorem)

3.4 Strong Consistency

3.4.1 Theorems from probability theory:

Theorem 3.2 (Strong Law of Large Numbers) Let \(Z_1, Z_2, \cdots\) be \(i.i.d\) real valued random variables, and \(E(Z_i) = m\). Then \(\frac{1}{n} \sum_{i=1}^n (Z_i - m) \to 0\) almost surely as \(n \to \infty\).

Theorem 3.3 (Central Limit Theorem) (It quantifies in a sense how fast is the convergence in the LLN)

Suppose \(Var(Z_i) = \sigma^2 < \infty\) for \(\{Z_i\}\) in Theorem 3.2 , then \(\sqrt n (\frac{1}{n} \sum_{i=1}^n (Z_i - m)) \underset{d}{\to} N(0, \sigma^2)\).

Recall, what this means is that \(\forall t\in R\), we have:

\[ \underset{n\to \infty}{\operatorname{lim}} P(\frac{\sqrt n}{\sigma} [\frac{1}{n}\sum_{i=1}^n (Z_i - m)] > t) = \int_t^\infty \frac{e^{-s^2/2}}{\sqrt {2\pi}} ds = 1-F(t) \]

Remark. CLT is still asymptotic (渐近的).

Theorem 3.4 (Berry-Essen Theorem) (It is a quantitative and non-asymptotic version of CLT)

\(\forall t\), we have: \[ \Big| P(\frac{\sqrt n}{\sigma} [\frac{1}{n}\sum_{i=1}^n (Z_i - m)] \geq t) - \int_t^\infty \frac{e^{-s^2/2}}{\sqrt {2\pi}} ds \Big| \leq \frac{c \gamma}{\sigma^3 \sqrt{n}}, \]

where \(\gamma = E(|Z_1|^3) < \infty\).

Remark. Berry-Essen Theorem doesn’t provide very precise information about \(P(\frac{\sqrt n}{\sigma} [\frac{1}{n}\sum_{i=1}^n (Z_i - m)] \geq t)\) when \(t\) is very large.

3.4.2 Concentration Inequalities

Goal: To quantify precisely what is the behavior of \(P(\frac{\sqrt n}{\sigma} \sum_{i=1}^n (Z_i - m) \geq t)\) (tail information).
What do we want more precisely: If \(\frac{\sqrt n}{\sigma} [\frac{1}{n}\sum_{i=1}^n (Z_i - m)]\) was truly a standard Gaussian random variable \(Z\), in that case what can we say about \(P(Z \geq t)\)?
What we could say is that \(P(Z \geq t) \leq e^{-\frac{t^2}{2}}\), \(\forall t > 0\).
The concentration inequalities we are after should give us some information similar to the one above.
To get there, let us start with the basics: For a given real valued random variable \(W\), what can we say about \(P(W \geq t)\) for \(t \geq 0\)?

Theorem 3.5 (Markov Inequality)

Let \(t > 0\), then we have

\[ P(W \geq t) \leq E(\frac{W}{t} ~1_{W \geq t}) \leq \frac{E[|W|]}{t} \]

Proof. \[ \begin{aligned} P(W \geq t) &= E[1_{W \geq t}]\\ &\leq E[\frac{W}{t} ~1_{W \geq t}]\\ &\leq E[\frac{|W|}{t} ~1_{W \geq t}]\\ &\leq E[\frac{|W|}{t}]. \end{aligned} \]

Remark. Let \(\phi: R \to [0,\infty)\) be non-decreasing. Then \(\forall t>0\):

\[ \begin{aligned} P(W \geq t) \leq P\Big(\phi(W) \geq \phi(t)\Big) \underset{M.I.}{\leq} \frac{E[\phi(W)]}{\phi(t)} \end{aligned} \]

How about we select \(\phi\) to be \(\phi(t) := exp(t \cdot s)\), where \(s>0\). Then \(\forall s>0\):

\[ P(W \geq t) \leq \frac{E[exp(sW)]}{exp(st)} = exp(-st)E[exp(sW)]. \]

As a result, we have:

\[ P(W \geq t) \leq \underset{s>0}{\operatorname{inf}}\{exp(-st) E[exp(sW)]\} \text{ (Chernoff's bound)}. \]

It is clear that we need to understand the behavior of \(E[exp(sW)]\).

The \(W\) we want to apply this to, for example, \(W:=\frac{1}{n} \sum_{i=1}^n (Z_i - m)\), where the \(Z_i\)s are independent with mean \(m\). Thus, the \(W\) for us should be of the form \(\sum_{i=1}^n Z_i\), where \(Z_i\)s are independent and \(E(Z_i) = 0\).

Lemma 3.2 Suppose \(Z\) is a r.v. with \(E(Z) = 0\) and \(\exists \text{ constant } a,b\), \(s.t. ~a\leq Z \leq b\) (Consequently, \(a<0\) and \(b>0\)). Then \(\forall s>0\), we have

\[ E[exp(sZ)] \leq exp(\frac{s^2(b-a)^2}{8}) \]

Remark. This lemma actually is saying that a bounded random variable is a sub-Gaussian random variable.
We say that a random variable \(Z\) (with \(E(Z) = 0\)) is sub-Gaussian with parameter \(\sigma^2\) if

\[ E(e^{sZ}) \leq exp(\frac{\sigma^2 s^2}{2}), ~s > 0 \]

The right hand side is exactly the moment generating function of a \(N(0, \sigma^2)\).

In particular, the lemma is saying that \(Z\) satisfying \(a\leq b\) and \(E(Z) = 0\) is sub-Gaussian with parameter \(\frac{(b-a)^2}{4}\).

Proof. Let \(Z = \frac{b-Z}{b-a} a + \frac{Z-a}{b-a} b\), then we have

\[ \begin{aligned} E[exp(sZ)] &= E \Big[ exp[s(\frac{b-Z}{b-a} a + \frac{Z-a}{b-a} b)] \Big] \\&\underset{convexity}{\leq} E[\frac{b-Z}{b-a} exp(sa) + \frac{Z-a}{b-a} exp(sb)] \\&\underset{E(Z) = 0}{=} \frac{b}{b-a} exp(sa) - \frac{a}{b-a} exp(sb) \end{aligned} \]

Let \(q = -\frac{a}{b-a}\), then \(\frac{b}{b-a} = 1-q\). Then,

\[ \begin{aligned} E[exp(sZ)] &\leq (1-q) ~exp(-s(b-a)q) + q ~exp(s(b-a)(1-q))\\ &= exp[-s(b-a)q + log\Big((1-q) + q~exp(s(b-a))\Big)] \end{aligned} \]

Let \(\psi(h):= -qh + log\Big( (1-q) + q ~exp(h)\Big)\), then \(\psi(0)=0\), \(\psi'(0) = 0\), \(\psi''(h) \leq \frac{1}{4} ~\forall h > 0\). By Taylor’s Theorem, \(\psi(h) \leq \frac{1}{2} (\frac{1}{4} h^2) = \frac{h^2}{8}\). As a result,

\[ E[exp(sZ)] \underset{h = s(b-a)}{\leq} exp(\frac{s^2(b-a)^2}{8}) \]

Theorem 3.6 (Hoeffding's Inequality) Let \(Z_1, \cdots, Z_n\) be independent random variable (not necessarily identically distributed) such that:

• \(E(Z_i) = 0\), \(\forall i=1,\cdots, n\);

• \(\forall i\), \(\exists \text{ constant } a_i, b_i\), \(s.t. ~a_i \leq Z_i \leq b_i\).

Then \(\forall t\), we have:

\[ P(\frac{1}{n} \sum_{i=1}^n Z_i \geq t) \leq exp(\frac{-2t^2n^2}{\sum_{i=1}^n (b_i - a_i)^2}) \]

Proof. Let \(W = \frac{1}{n} \sum_{i=1}^n Z_i\), then

\[ P(W \geq t) \underset{\text{Chernoff's Inequality}}{\leq} \underset{s>0}{\operatorname{inf}} \{\frac{E[e^{\frac{s}{n} \sum_{i=1}^n Z_i}]}{e^{st}}\}, \] where

\[ E[e^{\frac{s}{n} \sum_{i=1}^n Z_i}] = E\Big[\prod_{i=1}^n e^{\frac{s}{n} Z_i}\Big] \underset{independence}{=} \prod_{i=1}^n E[e^{\frac{s}{n} Z_i}] \]

Using Lemma 3.2, we have:

\[ \prod_{i=1}^n E[e^{\frac{s}{n} Z_i}] \leq \prod_{i=1}^n exp(\frac{s^2(b_i-a_i)^2}{8n^2}) = exp(\frac{s^2}{8n^2} \sum_{i=1}^n (b_i-a_i)^2) \]

Therefore,

\[ P(W \geq t) \leq \underset{s>0}{\operatorname{inf}} \{\frac{exp(\frac{s^2}{8n^2} \sum_{i=1}^n (b_i-a_i)^2)}{exp(st)}\} = \underset{s>0}{\operatorname{inf}} \{exp(\frac{s^2}{8n^2} \sum_{i=1}^n (b_i-a_i)^2 - st)\} \]

For the quadratic, \(s^* = \frac{4tn^2}{\sum_{i=1}^n (b_i-a_i)^2}\) minimizes it. As a result,

\[ P(W \geq t) \leq exp(\frac{-2t^2n^2}{\sum_{i=1}^n (b_i - a_i)^2}) \]

Remark.

1. The \(Z_i\)s can have different distributions with \(E(Z_i) = 0\) and \(a_i \leq Z_i \leq b_i\). Independence is essential though.

2. What if \(E(Z_i) \neq 0\)? Let \(\tilde Z_i := Z_i - E(Z_i)\) and \(a_i \leq \tilde Z_i \leq b_i\). Then \(\forall t>0\), we have:

\[ P(\frac{1}{n} \sum_{i=1}^n (Z_i - E(Z_i)) > t) = P(\frac{1}{n} \sum_{i=1}^n \tilde Z_i > t) \leq exp(\frac{2n^2 t^2}{\sum_{i=1}^n (b_i - a_i)^2}) \]

3. \(\forall t > 0\), we have:
   \[ \begin{aligned} P(\frac{1}{n} \sum_{i=1}^n (Z_i - E(Z_i)) > t) &\leq exp(\frac{2n^2 t^2}{\sum_{i=1}^n (b_i - a_i)^2}) \end{aligned} \]
   and
   \[ \begin{aligned} P(\frac{1}{n} \sum_{i=1}^n (E(Z_i) - Z_i) \geq t) &\leq exp(\frac{2n^2 t^2}{\sum_{i=1}^n (b_i - a_i)^2}) \end{aligned} \]
   As a result,
   \[ \begin{aligned} P\Big(|\frac{1}{n} \sum_{i=1}^n (Z_i - E(Z_i))| \geq t \Big) &\leq P(\frac{1}{n} \sum_{i=1}^n (Z_i - E(Z_i)) > t) + P(\frac{1}{n} \sum_{i=1}^n (E(Z_i) - Z_i) \geq t) \\ &\leq 2~exp(\frac{2n^2 t^2}{\sum_{i=1}^n (b_i - a_i)^2}) \end{aligned} \]

4. Suppose all \(Z_i\)s come from the same distribution, say Uniform or Gaussian. According to Theorem 3.6, the right hand side (\(exp(\frac{2n^2 t^2}{\sum_{i=1}^n (b_i - a_i)^2})\)) would be the same in both cases, which means that Hoeffding’s does not use variance information.

Theorem 3.7 (Bernstein's Inequality) Let \(Z_1, \cdots, Z_n\) be independent random variables with \(E(Z_i) = 0\) and such that \(-M \leq Z_i \leq M\), and let \(\sigma_i^2 = Var(Z_i)\), \(\forall i = 1,\cdots,n\). Then \(\forall t>0\), we have:

\[ P(\frac{1}{n} \sum_{i=1}^n Z_i \geq t) \leq exp(\frac{-\frac{1}{2} t^2n^2}{\frac{1}{3} Mnt + \sum_{i=1}^n \sigma_i^2}) \]

and

\[ P\Big(| \frac{1}{n} \sum_{i=1}^n Z_i | \geq t\Big) \leq 2~exp(\frac{-\frac{1}{2} t^2n^2}{\frac{1}{3} Mnt + \sum_{i=1}^n \sigma_i^2}) \]

Remark. Suppose \(\forall i\), \(\sigma_i^2 < \sigma^2\), then we have

\[ P(\frac{1}{n} \sum_{i=1}^n Z_i \geq t) \leq exp(\frac{-\frac{1}{2} t^2n}{\frac{1}{3} Mt + \sigma^2}) \]

• Hoeffding’s v.s. Bernstein’s:
  Let \(a_i = -M\), \(b_i = M\), \(\sigma^2 = Var(Z_i)\). Then for Hoeffding’s, we have:
  \[ \begin{aligned} P(\frac{1}{n} \sum_{i=1}^n Z_i \geq t) &\leq exp(\frac{-2t^2n^2}{\sum_{i=1}^n (b_i - a_i)^2})\\ &= exp(\frac{-2t^2n^2}{4n M^2})\\ &= exp(\frac{-t^2n}{2M^2}) \end{aligned} \]
  For Bernstein’s, we have:
  \[ \begin{aligned} P(\frac{1}{n} \sum_{i=1}^n Z_i \geq t) &\leq exp(\frac{-\frac{1}{2} t^2n^2}{\frac{1}{3} Mnt + \sum_{i=1}^n \sigma^2})\\ &= exp(\frac{-\frac{1}{2} t^2n}{\frac{1}{3} Mt + \sigma^2}) \end{aligned} \]
  As
  \[ \frac{-\frac{1}{2} t^2n}{\frac{1}{3} Mt + \sigma^2} \leq \frac{-\frac{1}{2}t^2n}{M^2} \Leftrightarrow M^2 \geq \sigma^2 + \frac{1}{3}Mt \]
  which means that \(M^2 \geq \sigma^2 + \frac{1}{3} Mt, ~\forall t \in [0,M]\), or \(\frac{2}{3}M^2 \geq \sigma^2\).
  As a result, when \(\sigma^2\) is considerably smaller than \(M^2\), we should use Bernstein’s Inequality rather than Hoeffding’s Inequality.
  In general, both inequalities have the form of
  \[ P(| W_n - E(W_n) | \geq t) \leq 2 ~exp(\cdots) \]
  i.e. what is the likelihood that some variable is away from its mean more than distance \(t\).

• Summary: all of these are theorems about sums of independent random variable.

3.4.3 More about Con-Ineq

Let \(Z_1, \cdots, Z_n\) be real-valued random variables. Also that \(U_1, \cdots, U_n\) be another sequence of random variables (not necessarily real-valued). We say \(\{Z_i\}_{i=1,\cdots,n}\) is a martingale difference sequence w.r.t. \(\{U_i\}_{i=1,\cdots,n}\) if

1. \(Z_k = h_k(U_1, \cdots, U_k)\), \(\forall k=1,\cdots,n\)

2. \(E(Z_{k+1} | U_1, \cdots, U_k) = 0\), \(\forall k = 1,\cdots, n-1\).

Remark. Suppose that \(Z_1, \cdots, Z_n\) are independent random variables with mean 0 and \(U_i = Z_i\), \(\forall i=1,\cdots,n\). Then \(\{Z_i\}_{i=1,\cdots,n}\) is a MDS w.r.t. (relative to) \(\{U_i\}_{i=1,\cdots,n}\)

Theorem 3.8 (Hoeffding's Inequality for MDS)

1. Let \(\{Z_i\}_{i=1,\cdots,n}\) be a MDS relative to \(\{X_i\}_{i=1,\cdots,n}\) (which generalizes “Let \(\{Z_i\}_{i=1,\cdots,n}\) be independent r.v.s with mean 0”).

2. Assume that \(\forall i=1,\cdots, n\), we have:
   \[ V_i \leq Z_i \leq V_i + C_i, \]
   where \(C_i >0\) is a fixed number, and \(V_i\) can be a r.v. and \(V_i = \psi_i(X_1, \cdots, X_{i-1})\), \(\forall i\) (which generalizes the assumption \(a_i \leq Z_i \leq b_i\)).

Then, \(\forall t>0\), we have:

\[ P(\frac{1}{n}\sum_{i=1}^n Z_i \geq t) \leq exp(\frac{-2t^2n^2}{\sum_{i=1}^n C_i^2}) \]

Theorem 3.9 (McDiarmid's Inequality) Let \(X_1, \cdots, X_n\) be independent r.v.s in \(R^d\). Suppose we have a function \(g: (R^d)^n \to R\), i.e. \(g(x_1, \cdots, x_n) \in R, ~x_1, \cdots, x_n \in R^d\), satisfying: \(\forall i=1,\cdots, n\),

\[ \underset{x_1, \cdots, x_n, x_i'}{\operatorname{sup}} \Big| g(x_1, \cdots, x_n) - g(x_1, \cdots, x_{i-1}, x_i', x_{i+1}, \cdots, x_n) \Big| \leq C_i. \]

Then we have:

\[ P(W_n - E(W_n) \geq t) \leq exp(\frac{-2t^2}{\sum_{i=1}^n C_i^2}), \]

where \(W_n := g(X_1, \cdots, X_n)\).

Proof.

Idea: To show that \(W_n - E(W_n) = \sum_{i=1}^n Z_i\) for a suitable MDS satisfying the assumptions in Theorem 3.8.

Let \(Z_k:= E(W_n | X_1, \cdots, X_k) - E(W_n | X_1, \cdots, X_{k-1})\), \(k \geq 2\); \(Z_1 := E(W_n | X_1) - E(W_n)\). Then we have:

1. we can write \(W_n - E(W_n) = \sum_{i=1}^n Z_i\):
   \[ \begin{aligned} \sum_{i=1}^n Z_i &= E(W_n | X_1, \cdots, X_n) - E(W_n)\\ &= E(g(X_1, \cdots, X_n) | X_1, \cdots, X_n) - E(W_n)\\ &= g(X_1, \cdots, X_n)- E(W_n)\\ &= W_n- E(W_n) \end{aligned} \]

2. \(\{Z_i\}\) is a MDS relative to \(\{X_i\}\):
   \[ \begin{aligned} Z_k &= E(W_n | X_1, \cdots, X_k) - E(W_n | X_1, \cdots, X_{k-1})\\ &= \tilde h_k(X_1, \cdots, X_k) - \tilde h_{k-1}(X_1, \cdots, X_{k-1})\\ &= h_k(X_1, \cdots, X_k) \end{aligned} \]
   and
   \[ \begin{aligned} E(Z_{k+1} | X_1, \cdots, X_k) &= E\Big(E(W_n |X_1, \cdots, X_{k+1}) - E(W_n | X_1, \cdots, X_k) \Big| X_1, \cdots, X_k \Big)\\ &= E\Big( E(W_n |X_1, \cdots, X_{k+1}) \Big | X_1, \cdots, X_k\Big) - E\Big( E(W_n |X_1, \cdots, X_k) \Big | X_1, \cdots, X_k\Big)\\ &\underset{\text{Tower Property}}{=} E(W_n |X_1, \cdots, X_k) - E(W_n |X_1, \cdots, X_k)\\ &= 0 \end{aligned} \]

3. we can bound \(V_k \leq Z_k \leq V_k + C_k\) for some \(V_k, C_k\):
   (Show that in HW2)

3.4.4 Strong Consistency

Statements that may encounter (\(P(|W_n - E(W_n)| \geq t) \leq 2 exp(-cnt^2)\)):

1. With probability greater than \(1-\delta\), we have: \(|W_n - E(W_n)| \leq f(\delta, n)\) (fixing threshold)

2. With probability greater than \(1-\delta\), we have: \(|W_n - E(W_n)| \leq \sqrt{\frac{1}{cn} log(\frac{2}{\delta})}\) (let \(\delta = 2 exp(-cnt^2)\), i.e. fixing probability)

Theorem 3.10 (Borel-Cantelli Theorem) Let \(E_1, E_2, \cdots\) be events in a probability space \((\Omega, \mathcal F, P)\), \(\sum_{i=1}^\infty P(E_i) \leq \infty\) (the events \(E_i\) become less and less likely), then for \(E=\{\omega \in \Omega: ~\exists N(\omega), s.t. ~ \forall n \geq N(\omega), \omega \in E_n^c\}\), we have \(P(E) = 1\).

Example 3.9 \(Z_1, Z_2, \cdots\) independent and \(Z_i \sim Bernoulli(p_i)\), \(\sum_{i=1}^\infty p_i < \infty\). Notice \(p_i = P(Z_i=1) \to 0\) as \(i \to \infty\).

Example 3.10 \(Z_1, Z_2, \cdots\) are i.i.d. r.v.s with mean \(m\) and \(|Z_i| \leq M\), \(\forall i=1,2,\cdots\)

By Hoeffding’s Inequality, \(\forall t>0\), we have:

\[ P(|\frac{1}{n}\sum_{i=1}^n Z_i - m| \geq t) \leq 2 ~exp(\frac{-nt^2}{2M^2}) \]

The idea is to define a sequence \(\{t_n\}_{n\in N}\) such that \(t_n \to 0\) and \(\sum_{n=1}^\infty 2 ~exp(\frac{-nt_n^2}{2M^2}) < \infty\).

Then let \(E_n := \{|\frac{1}{n}\sum_{i=1}^n Z_i - m| \geq t_n \}\). As a result, \(\sum_{n=1}^\infty P(E_n) \leq 2~exp(\frac{-nt^2}{2M^2}) < \infty\).

By Borel-Cantelli: \(P(E) = 1\), where \(E = \{\omega \in \Omega: \forall n \text{ large enough, } \omega \in E_n^c \}\).

Therefore, what we are saying is that for almost every \(\omega \in \Omega\), \(\forall\) large enough \(n\), we have \(|\frac{1}{n}\sum_{i=1}^n Z_i - m| \leq t_n\).

As \(t_n \to 0\), we then have for almost every \(\omega \in \Omega\), \(\underset{n \to \infty}{\operatorname{lim}} |\frac{1}{n}\sum_{i=1}^n Z_i - m| = 0\).

For example, \(t_n := \sqrt{4M^2 \frac{log(n)}{n}}\) satisfies the above assumptions.

Theorem 3.11 Let \(\hat{\mathfrak f}_n\) be a histogram classifier built from data \((x_1, y_1), \cdots, (x_n, y_n)\). Let \(h_n\) be the length-scale associated to \(\hat{\mathfrak f}_n\). If \(\begin{cases} h_n \to 0 ~as~ n\to \infty\\ nh_n^d \to \infty ~as~ n \to \infty\end{cases}\), then \(\{\hat{\mathfrak f}_n\}\) is universally strong consistent.

Proof. Recall histogram classifiers 3.5

\(\forall z\in R^d\), denote \(A_n(z)\) by the cell in the grid that contains \(z\). Then, \(\omega_{in}(X) = \frac{1_{A_n(X)}(x_i)}{N_n(X)}\), where \(1_{A_n(X)}(x_i) := \begin{cases}1&x_i \in A_n(X)\\0&o.w. \end{cases}\), \(N_n(X):= \#\{j ~s.t. 1_{A_n(X)}(x_j)=1 \}\).

As \(\hat \eta_n(X) = \sum_{i=1}^n Y_i \omega_{in}(X) = \sum_{i=1}^n Y_i \frac{1_{A_n(X)}(x_i)}{N_n(X)}\), we have

\[ \hat \eta_n(X) \geq \frac{1}{2} \Leftrightarrow \sum_{i=1}^n Y_i1_{A_n(X)}(x_i) \geq \sum_{i=1}^n (1-Y_i)1_{A_n(X)}(x_i) \]

Let \(\rho_X(A_n(x)):= P_{(X,Y) \sim \rho} (X\in A_n(x))\), \(\hat \alpha_n^0(x):= \frac{\sum_{i=1}^n (1-Y_i) 1_{A_n(X)}(x_i)}{n\rho_X(A_n(x))}\), \(\hat \alpha_n^1(x):=\frac{\sum_{i=1}^n Y_i 1_{A_n(X)}(x_i)}{n\rho_X(A_n(x))}\), then

\[ \hat \eta_n(x) \geq \frac{1}{2} \Leftrightarrow \hat \alpha_n^0(x) \geq \hat \alpha_n^1(x) \]

It can be shown that \(R(\hat{\mathfrak f}_n) - R^* \leq E_{(X,Y)\sim \rho} \Big[|1-\eta(X) - \hat \alpha_n^0(X)|\Big] + E_{(X,Y)\sim \rho} \Big[|\eta(X) - \hat \alpha_n^1(X)|\Big]\) (use \(\hat \alpha_n^0(X)\) to estimate \(1-\eta(X)\) and use \(\hat \alpha_n^1(X)\) to estimate \(\eta(X)\)).

Let

\[ \begin{aligned} g_n((x_1, y_1), \cdots, (x_n, y_n)) &= E_{(X,Y)\sim \rho} \Big[|\eta(X) - \hat \alpha_n^1(X)|\Big]\\ &= g_n((x_1, y_1), \cdots, (x_n, y_n)) - E_{(x_1, y_1), \cdots, (x_n, y_n)[g_n((x_1, y_1), \cdots, (x_n, y_n))]} \text{ (variance)}\\ &+E_{(x_1, y_1), \cdots, (x_n, y_n)[g_n((x_1, y_1), \cdots, (x_n, y_n))]} \text{ (bias)} \end{aligned} \]

then for the bias term, it goes to 0 as \(n \to \infty\) following a slight generalization of Stone’s Theorem since here weights don’t exactly add to 1.

For the variance term, we have:

\[ \begin{aligned} g_n((x_1, y_1), \cdots, (x_i,y_i),\cdots, (x_n, y_n)) &= E_{(X,Y) \sim \rho}\Big[ |\eta(X) - \frac{\sum_{k=1}^n y_k 1_{A_n(X)}(x_k)}{n\rho_X(A_n(x))}| \Big]\\ &= E_{(X,Y) \sim \rho}\Big[ |\eta(X) - \frac{\sum_{k\neq i} y_k 1_{A_n(X)}(x_k)}{n\rho_X(A_n(x))} + \frac{y_i 1_{A_n(X)}(x_i)}{n\rho_X(A_n(x))}| \Big] \end{aligned} \]

and

\[ \begin{aligned} g_n((x_1, y_1), \cdots, (x_i',y_i'),\cdots, (x_n, y_n)) &= E_{(X,Y) \sim \rho}\Big[ |\eta(X) - \frac{\sum_{k\neq i} y_k 1_{A_n(X)}(x_k)}{n\rho_X(A_n(x))} + \frac{y_i' 1_{A_n(X)}(x_i')}{n\rho_X(A_n(x))}| \Big] \end{aligned} \]

As a reuslt,

\[ \begin{aligned} | g_n((x_1, y_1), \cdots, (x_i,y_i),\cdots, (x_n, y_n)) -\\ g_n((x_1, y_1), \cdots, (x_i',y_i'),\cdots, (x_n, y_n))| &\leq E_{(X,Y)\sim \rho}[\frac{y_i 1_{A_n(X)}(x_i)}{n\rho_X(A_n(x))} + \frac{y_i' 1_{A_n(X)}(x_i')}{n\rho_X(A_n(x))}]\\ &\underset{x_i \in A_n(X) \Leftrightarrow X \in A_n(x_i)}{\leq} E[\frac{1_{A_n(x_i)}(X)}{n\rho_X(A_n(x_i))}] + E[\frac{1_{A_n(x_i')}(X)}{n\rho_X(A_n(x_i'))}]\\ &= \frac{1}{n \rho_X(A_n(x_i))}P(X\in A_n(x_i)) + \frac{1}{n \rho_X(A_n(x_i'))}P(X\in A_n(x_i'))\\ &= \frac{2}{n} \end{aligned} \]

Let \(C_i = \frac{2}{n}\), by McDiarmid’s Inequality, we have:

\[ \begin{aligned} P(|g_n - E[g_n]| \geq t) &\leq 2~exp(\frac{-2t^2}{n\sum C_i^2})\\ &= 2~exp(-\frac{1}{2}nt^2) \end{aligned} \]

Let \(t_n:= \sqrt{c \frac{log(n)}{n}}\), where we can choose \(C\) large enough so that by Borel-Cantelli Theorem, we have: with probability 1, \(\forall\) large enough \(n\), we have \(|g_n - E[g_n]| \leq t_n\). As a result, we have \(|g_n - E[g_n]| \to 0\) as \(n \to \infty\) a.s.