Chapter 6 Linear Classifiers
\(\mathcal F = \{\text{all linear classifiers}\}\), \(\mathcal X = R^d\), \(\mathcal Y = \{-1,1\}\) or \(\{1,\cdots,K\}\). Consider mainly on binary case.
Let \(\beta \in R^d\) and \(\beta_0 \in R\), \(\mathcal H_{\beta, \beta_0} = \{x\in R^d: <\beta, x> + \beta_0 = 0\}\) (hyperplane), \(\mathcal H^+_{\beta, \beta_0} = \{x\in R^d: <\beta, x> + \beta_0 \geq 0\}\) and \(\mathcal H^-_{\beta, \beta_0} = \{x\in R^d: <\beta, x> + \beta_0 < 0\}\) (half plane).
\[ \mathfrak f_{\beta, \beta_0}(x):=\begin{cases}1 & <\beta,x> + \beta_0 \geq 0 (\Leftrightarrow x \in H^+_{\beta,\beta_0})\\- 1& <\beta,x> + \beta_0 < 0(\Leftrightarrow x \in H^-_{\beta,\beta_0})\end{cases} \]
- Question: How to find a linear classifier based on \((x_i, y_i)\), \(i=1,\cdots,n\).
A: Three different ways to tune \(\beta, \beta_0\) from data: LDA (linear discriminant analysis) or QDA (quadratic discriminant analysis), Logistic Regression, Perceptrons and SVMs.
6.1 LDA or QDA
Let \(\mathcal Y = \{1, \cdots, K\}\), \((X,Y) \sim \rho\), where \(P(Y=k) = \omega_k, \rho_{X|Y}(X | Y=k) = N(\mu_k, \Sigma_k)\), we have:
\[ \begin{aligned} \mathfrak f_{Bayes}(x) &= \underset{k=1,\cdots, K}{\operatorname{argmax}} P(Y=k | X=x)\\ &= \underset{k=1,\cdots, K}{\operatorname{argmax}} \frac{\rho_{X|Y}(x | Y=k) \cdot \omega_k}{\rho_X(x)}\\ &= \underset{k=1,\cdots, K}{\operatorname{argmax}} [\rho_{X|Y}(x | Y=k) \cdot \omega_k]\\ &= \underset{k=1,\cdots, K}{\operatorname{argmax}} [log\Big (\rho_{X|Y}(x | Y=k)\Big ) + log(\omega_k)]\\ &= \underset{k=1,\cdots, K}{\operatorname{argmin}} [-log\Big (\frac{1}{(2\pi)^{d/2} (det(\Sigma_k))^{1/2}} \Big ) + \frac{1}{2} <\Sigma_k^{-1} (x-\mu_k), (x-\mu_k)> - log(\omega_k)]\\ &:= \underset{k=1,\cdots, K}{\operatorname{argmin}} \delta_k(x) \end{aligned} \]
Observation: \(\delta_k(x)\) is quadratic and convex in \(x\).
QDA: What if we only have \((x_i, y_i)\), \(i=1,\cdots,n\)? We use the observations to estimate \(\mu_k, \omega_k, \Sigma_k\), \(k=1,\cdots, K\).
Example 6.1 \[ \hat \mu_k := \frac{\sum_{i ~s.t. ~y_i=k} x_i}{\#\{x_i ~s.t. ~y_i=k\} ~(:= N_k)} \]
\[ (\hat \Sigma_k)_{lm} := (\frac{1}{N_k} \sum_{i ~s.t. ~y_i=k} x_{il}x_{im} - \hat \mu_{kl} \hat \mu_{km}), \text{ where } l=1,\cdots,d, ~m=1,\cdots,d. \]
\[ \hat \omega_k = \frac{N_k}{n} \]
\[ \hat \delta_k(x) \text{ same as } \delta_k \text{ but with } \hat{} \text{ everywhere} \]
LDA: What if we had assumed \(\Sigma_1 = \Sigma_2 = \cdots = \Sigma_K = \Sigma\)?
\[ \begin{aligned} \mathfrak f(x) &= \underset{k=1,\cdots, K}{\operatorname{argmin}} [\frac{1}{2} <\Sigma^{-1}x, x> + <\Sigma^{-1}x, \mu_k> + \frac{1}{2} <\Sigma^{-1}\mu_k, \mu_k> - log(\omega_k)]\\ &= \underset{k=1,\cdots, K}{\operatorname{argmin}} [<\Sigma^{-1}x, \mu_k> + \frac{1}{2} <\Sigma^{-1}\mu_k, \mu_k> - log(\omega_k)]\\ &:= \underset{k=1,\cdots, K}{\operatorname{argmin}} l_k(x), ~(l_k(x) \text{ is linear}) \end{aligned} \]
We can estimate \(\mu_k ,\omega_k\) by \(\hat \mu_k ,\hat \omega_k\), and \(\Sigma\) with the full data set.
6.2 Logistic Regression
Let \(\mathcal Y = \{1, \cdots, K\}\), \(\vec \beta_k \in R^d\), \(\beta_{0k} \in R\), and \((X,Y)\) satisfies: \(P(Y=k | X=x) = \frac{exp(<x,\vec \beta_k> + \beta_{0k})}{1 + \sum_{l=1}^{K-1} exp(<x,\vec \beta_l> + \beta_{0l})}\), \(P(Y=K | X=x) = \frac{1}{1 + \sum_{l=1}^{K-1} exp(<x,\vec \beta_l> + \beta_{0l})}\), where \(k=1,\cdots,K-1\). Let \(\varphi_k(x) := exp(<x,\vec \beta_k> + \beta_{0k})\) and \(\varphi_K(x):=1\), where \(k=1,\cdots,K-1\). Then we have:
\[ \begin{aligned} \mathfrak f_{Bayes} (x) &= \underset{k=1,\cdots, K}{\operatorname{argmax}} P(Y=k | X=x)\\ &= \underset{k=1,\cdots, K}{\operatorname{argmax}} \varphi_k(x)\\ &= \underset{k=1,\cdots, K}{\operatorname{argmax}} log(\varphi_k(x)) \end{aligned} \]
What if we only have observed \((x_i, y_i)\), \(i=1,\cdots,n\)? We use the observations to estimate the parameters.
Example 6.2 (MLE) Given the data, find the best parameters (the ones maximizing the likelihood of the observations), i.e.
\[ \{(\vec \beta_k^*, \beta_{0k}^*)\} = \underset{\{(\vec \beta_k, \beta_{0k})\}_{k=1,\cdots,K-1}}{\operatorname{max}} \prod_{i=1}^n P(Y = y_i | X = x_i) \]
6.3 Perceptrons and SVMs
Let \(\mathcal Y = \{-1, 1\}\), \((x_i, y_i)_{i=1,\cdots,n}\), \((\vec \beta, \beta_0)\), \(\mathfrak f_{\beta, \beta_0}(x):=\begin{cases}1 & <\beta,x> + \beta_0 \geq 0 (\Leftrightarrow x \in H^+_{\beta,\beta_0})\\- 1& <\beta,x> + \beta_0 < 0(\Leftrightarrow x \in H^-_{\beta,\beta_0})\end{cases}\), \(\sigma(\vec \beta, \beta_0) := \sum_{i \in \mathcal M_{\vec \beta, \beta_0}} dist(x_i, \mathcal H_{\vec \beta, \beta_0})\), where \(\mathcal M_{\vec \beta, \beta_0} = \{i \text{ s.t. } \mathfrak f_{\vec \beta, \beta_0} (x_i) \neq y_i\}\)
6.3.1 Perceptrons
Let \((\vec \beta^*, \beta_0^*) := \underset{(\vec \beta, \beta_{0})}{\operatorname{min}} \sigma(\vec \beta, \beta_0)\), then the perceptron classifier is \(\mathfrak f_{\vec \beta^*, \beta_0^*} (x)\). There exist many solutions of perceptron problems but some hyperplanes seem to be more robust:
Example 6.3 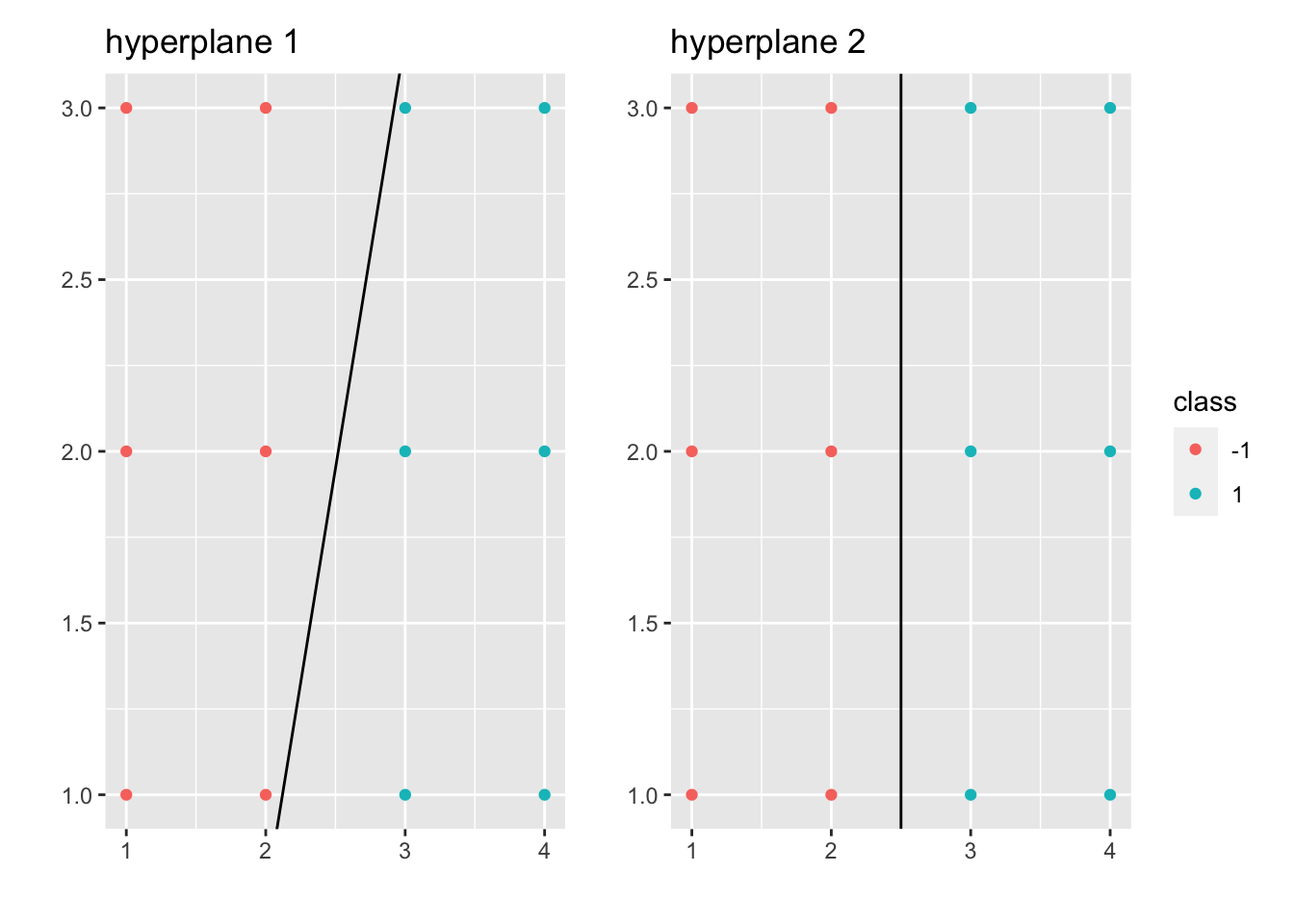
Hyperplane 2 seems to be more robust.